Lifeboat Foundation: Safeguarding Humanity
Toggle light / dark theme

Blog – Page 10

This approach significantly enhances performance, as observed in Atari video games and several other tasks involving multiple potential outcomes for each decision.

“They basically asked what happens if rather than just learning average rewards for certain actions, the algorithm learns the whole distribution, and they found it improved performance significantly,” explained Professor Drugowitsch.

In the latest study, Drugowitsch collaborated with Naoshige Uchida, a professor of molecular and cellular biology at Harvard University. The goal was to gain a better understanding of how the potential risks and rewards of a decision are weighed in the brain.

Read more | >

Using machine learning, a team of researchers in Canada has created ultrahigh-strength carbon nanolattices, resulting in a material that’s as strong as carbon steel, but only as dense as Styrofoam.

The team noted last month that it was the first time this branch of AI had been used to optimize nano-architected materials. University of Toronto’s Peter Serles, one of the authors of the paper describing this work in Advanced Materials, praised the approach, saying, “It didn’t just replicate successful geometries from the training data; it learned from what changes to the shapes worked and what didn’t, enabling it to predict entirely new lattice geometries.”

To quickly recap, nanomaterials are engineered by arranging atoms or molecules in precise patterns, much like constructing structures with extremely tiny LEGO blocks. These materials often exhibit unique properties due to their nanoscale dimensions.

Read more | >

Scientists are exploring gene editing as a way to correct trisomy at the cellular level. Using CRISPR-Cas9, researchers successfully removed extra copies of chromosome 21 in Down syndrome cell lines, restoring normal gene expression.

This breakthrough suggests that, with further development, similar approaches could be applied to neurons and glial cells, offering a potential treatment for those with the condition.

Gene Editing for Trisomy Treatment.

Read more | >

But other calculations say that applies only in limited cases and that if you ramp up the warp engine slowly enough, you’ll be fine.

Yet more calculations sidestep all of this and just look at how much negative energy you actually need to construct your warp drive. And the answer is, for a single macroscopic bubble — say, 30 feet (100 meters) across — you would need 10 times more negative energy than all of the positive energy contained in the entire universe, which isn’t very promising.

However, still other calculations show that this immense amount applies only to the traditional warp bubble as defined by Alcubierre. It might be possible to reshape the bubble so there’s a tiny “neck” in the front that’s doing the work of compressing space and then it balloons out to an envelope to contain the warp bubble. This minimizes any quantum weirdness so that you need only about a star’s worth of negative energy to shape the drive.

Read more | >

A massive dataset of 3,628 Type Ia Supernovae from the Zwicky Transient Facility is being released, offering new insights into cosmic expansion.

This unprecedented collection will refine how cosmologists measure distances and study dark energy. With high-precision data from cutting-edge telescopes, scientists aim to resolve discrepancies in the standard cosmological model and explore new physics.

A Game-Changing Dataset for Cosmology.

Read more | >

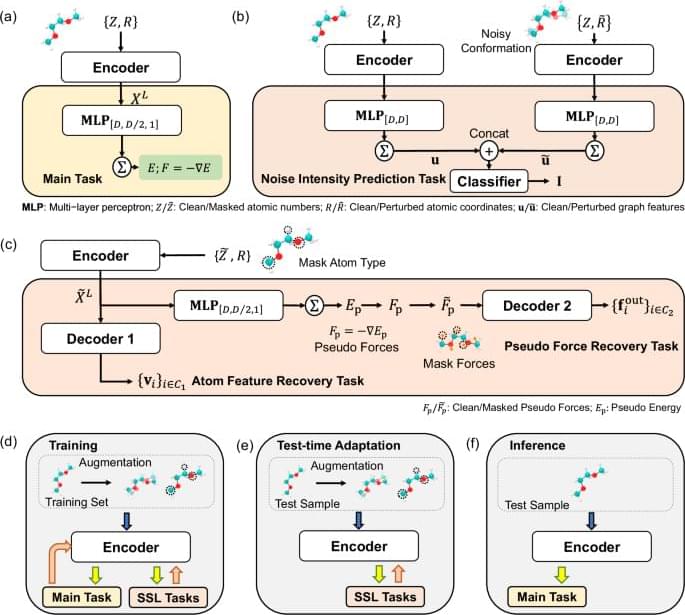
Molecular Dynamics (MD) simulation serves as a crucial technique across various disciplines including biology, chemistry, and material science1,2,3,4. MD simulations are typically based on interatomic potential functions that characterize the potential energy surface of the system, with atomic forces derived as the negative gradients of the potential energies. Subsequently, Newton’s laws of motion are applied to simulate the dynamic trajectories of the atoms. In ab initio MD simulations5, the energies and forces are accurately determined by solving the equations in quantum mechanics. However, the computational demands of ab initio MD limit its practicality in many scenarios. By learning from ab initio calculations, machine learning interatomic potentials (MLIPs) have been developed to achieve much more efficient MD simulations with ab initio-level accuracy6,7,8.

Despite their successes, the crucial challenge of implementing MLIPs is the distribution shift between training and test data. When using MLIPs for MD simulations, the data for inference are atomic structures that are continuously generated during simulations based on the predicted forces, and the training set should encompass a wide range of atomic structures to guarantee the accuracy of predictions. However, in fields such as phaseion9,10, catalysis11,12, and crystal growth13,14, the configurational space that needs to be explored is highly complex. This complexity makes it challenging to sample sufficient data for training and easy to make a potential that is not smooth enough to extrapolate to every relevant point. Consequently, a distribution shift between training and test datasets often occurs, which causes the degradation of test performance and leads to the emergence of unrealistic atomic structures, and finally the MD simulations collapse15.

Read more | >

In recent years, roboticists and computer scientists have developed a wide range of systems inspired by nature, particularly by humans and animals. By reproducing animal movements and behaviors, these robots could navigate real-world environments more effectively.

Researchers at Northeastern University in China recently developed a new H-shaped bionic robot that could replicate the movements that cheetahs make while running. This robot, introduced in a paper published in the Journal of Bionic Engineering, is based on piezoelectric materials, a class of materials that generate an electric charge when subjected to mechanical stress.

“The piezoelectric robot realizes linear motion, turning motion, and turning motion with different radii by the voltage differential driving method,” wrote Ying Li, Chaofeng Li and their colleagues in their paper. “A prototype with a weight of 38 g and dimensions of 150 × 80 × 31 mm3 was fabricated.”

Read more | >

The future is coming and much faster than we think. Let’s do an exercise of imagination, imagine, for a moment, being able to send information from one point to another without the need for cables, Wi-Fi or traditional signals, more or less like something telepathic, right? Well, that is precisely what scientists have recently achieved at the University of Oxford: teleporting data between two quantum computers. Although it may seem like science fiction or just news, the world.

Although, let’s lower the hype a little, the transmission distance of this experiment was less than two meters, but that doesn’t matter, what matters is having achieved this milestone of sharing information without the need for connections.

Read more | >

Imagine being able to see quantum objects with your own eyes — no microscopes needed. That’s exactly what researchers at TU Wien and ISTA have achieved with superconducting circuits, artificial atoms that are massive by quantum standards.

Unlike natural atoms, these structures can be engineered to have customizable properties, allowing scientists to control energy levels and interactions in ways never before possible. By coupling them, they’ve developed a method to store and retrieve light, laying the groundwork for revolutionary quantum technologies. These engineered systems also enable precise quantum pulses and act as a kind of quantum memory, offering an unprecedented level of control over light at the quantum level.

Gigantic Quantum Objects – Visible to the Naked Eye.

Read more | >

Among the most intriguing ideas is warp drive—a concept that challenges Einstein’s Theory of Relativity by suggesting faster-than-light travel might be possible by warping space and time.

In 1994, theoretical physicist Miguel Alcubierre introduced the idea of a space-time bubble that could contract distances ahead of a spacecraft while expanding them behind it. His model, known as the Alcubierre drive, suggested a loophole in relativity that could, in theory, allow faster-than-light travel. Yet, most scientists dismissed it as impossible due to extreme energy requirements.

Not everyone was ready to abandon the idea. Joseph Agnew, an undergraduate at the University of Alabama, set out to explore whether the theory held up mathematically. “If you fulfill all the energy requirements, they can’t prove that it doesn’t work,” he stated in a university press release.

Read more | >