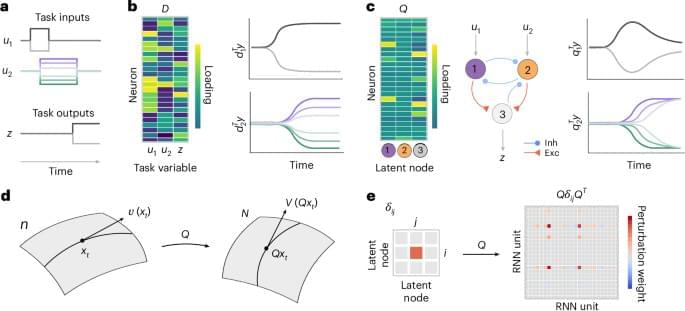
The latent circuit model captures task-related neural activity in the low-dimensional subspace spanned by the columns of Q, with dynamics within this subspace generated by the neural circuit Eq. (2). We infer the latent circuit parameters (Q, w_rec, w_in and w_out) from neural activity y by minimizing the loss function L = ∑_k,t ∥ y − Qx ∥ ₂ + ∥ z − w_outx ∥ ₂, where k and t index trials and time within a trial, respectively (Methods).

In the latent circuit model, the heterogeneity of single-neuron responses has three possible sources: mixing of task inputs to the latent circuit via w_in, recurrent interactions among latent nodes via w_rec and linear mixing of representations in single neurons via the embedding Q. The orthonormality constraint on Q implies that the projection defined by the transpose matrix Q^T is a dimensionality reduction in which projection onto the i th column of Q correlates with the activity of the i th node in the latent circuit. Conversely, the image of each latent node i is a high-dimensional activity pattern given by the column q_i of the matrix Q. Thus, the latent circuit provides a dimensionality reduction that incorporates an explicit mechanistic hypothesis for how the resulting low-dimensional dynamics are generated.

In general, it is not obvious under what circumstances we can satisfactorily fit a latent circuit model to the responses of a high-dimensional system. If, for example, solutions to cognitive tasks that emerge in large systems are qualitatively different from mechanisms operating in small circuits, then we should not be able to adequately fit task-related dynamics of the large system with a low-dimensional circuit model. However, the existence of a low-dimensional circuit solution that accurately captures dynamics of the large system would suggest that this circuit mechanism may be latent in the high-dimensional system.