The evolution of the human brain has long been framed in terms of sexual selection, with an emphasis on consistent but small on-average volumetric differences between males and females. In this revie…
Information geometry has emerged from the study of the invariant structure in families of probability distributions. This invariance uniquely determines a second-order symmetric tensor g and third-order symmetric tensor T in a manifold of probability distributions. A pair of these tensors (g, T) defines a Riemannian metric and a pair of affine connections which together preserve the metric. Information geometry involves studying a Riemannian manifold having a pair of dual affine connections. Such a structure also arises from an asymmetric divergence function and affine differential geometry. A dually flat Riemannian manifold is particularly useful for various applications, because a generalized Pythagorean theorem and projection theorem hold. The Wasserstein distance gives another important geometry on probability distributions, which is non-invariant but responsible for the metric properties of a sample space. I attempt to construct information geometry of the entropy-regularized Wasserstein distance.
With brain swaps and death rays, a little-known French sci-fi genre explored science’s dark possibilities a century ago
Green Corridors, LLC has received a permit from President Trump to build an elevated railway for autonomous vehicles between Laredo, Texas, and Monterrey, Mexico, promising reduced congestion times…
Green Corridors, LLC has received a permit from President Trump to build an elevated railway for autonomous vehicles between Laredo, Texas, and Monterrey, Mexico, promising reduced congestion times…
TOQUERVILLE, Washington County — The Hurricane-based robotics company IME Automation recently announced the purchase of 6.5 acres of land at Anderson Junction in Toquerville, where the company has broken ground for its new 20,000-square-foot facility.
IME Automation develops custom robotic systems for manufacturing operations worldwide. This new facility will expand its capabilities and footprint in the region.
The land was acquired approximately eight months ago during the summer of 2024, brokered by sales agent Brandon Price with the commercial real estate agency NAI Excel. Price said he delayed putting out information about the acquisition until IME Automation was completely ready to break ground.
DOI Not Found
Posted in futurism | Leave a Comment on DOI Not Found
The DOI entered is not a valid DOI: it should start with 10 followed by a dot, and contain a slash with no preceding whitespace.
The email address entered is invalid.
Please contact us if you wish to report this anyway.
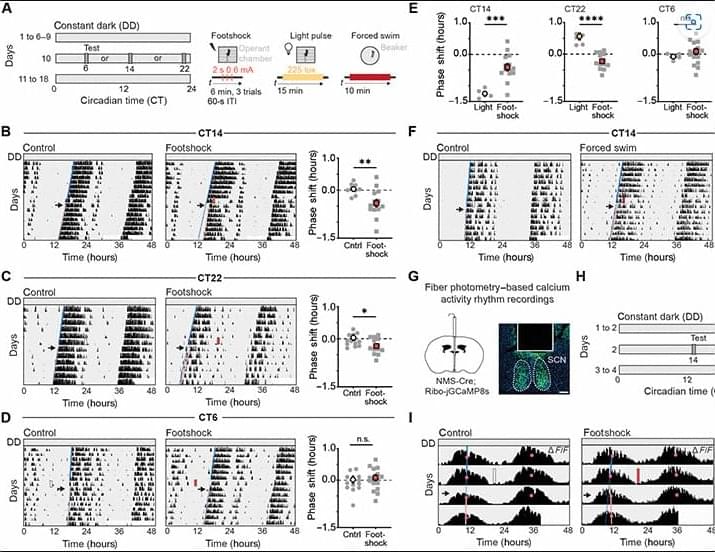
Stress, via the paraventricular thalamus, modifies the central pacemaker and interacts with light to influence circadian outputs.