Essentially this can lead to euclidean geometry in programming essentially allowing near infinite decompression either in programming or in devices or even spaceships.
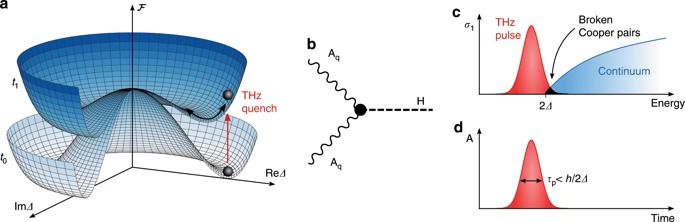
In physics and mathematics, in the area of vector calculus, Helmholtz’s theorem,[1][2] also known as the fundamental theorem of vector calculus,[3][4][5][6][7][8][9] states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational (curl-free) vector field and a solenoidal (divergence-free) vector field; this is known as the Helmholtz decomposition or Helmholtz representation. It is named after Hermann von Helmholtz.[10]
As an irrotational vector field has a scalar potential and a solenoidal vector field has a vector potential, the Helmholtz decomposition states that a vector field (satisfying appropriate smoothness and decay conditions) can be decomposed as the sum of the form − ∇ ϕ + ∇ × A {\displaystyle -\nabla \phi +\nabla \times \mathbf {A} }, where ϕ {\displaystyle \phi } is a scalar field called “scalar potential”, and A is a vector field, called a vector potential.
 , where ϕ {\displaystyle \phi } is a scalar field called “scalar potential”, and A is a vector field, called a vector potential.
, where ϕ {\displaystyle \phi } is a scalar field called “scalar potential”, and A is a vector field, called a vector potential.